오디오 필터(21)-FIR 카이저 윈도우(Kaiser window)
카이저 윈도우로 FIR 필터 구하기
FIR 필터를 구하는 방법 중에 윈도우 방법에서 카이저 윈도우(Kaiser window) 함수를 만들어서 기존의 윈도우 함수 대신 사용하는 것입니다. 카이저 윈도우는 필터를 만들기 위한 설계요건에 따라 윈도우 형태가 변경되는 특징이 있습니다. 이는 마치 IIR 필터의 통과 필터를 설계하는 방법을 FIR 필터로 옮긴것 같습니다.
카이저 윈도우 구하기
카이저 윈도우는 구현되는 필터의 조건에 따라서 윈도우를 형성하는 파라미터를 구해줘야 합니다.
- 윈도우의 통과 대역 주파수 $f_{pass}$와 저지 대역 주파수 $f_{stop}$과 통과 대역의 리플(ripple) $\delta_{pass}$와 저지 대역의 리플 $\delta_{stop}$, 샘플 주파수 $f_s$를 설정합니다.
- 필터의 차단 주파수는 $f_c = (f_{pass}+f_{stop})/2$로 구합니다.
- 그리고 두 개의 리플 중 작은 리플 값만 사용합니다.
- 리플과 통과 및 저지 대역 주파수를 가지고 원도우의 길이(M)과 윈도의 모양을 결정하는 파라미터인 $\beta$를 구합니다.
- M과 $\beta$를 가지고 베셀 함수(Bessel function)를 이용해서 카이저 윈도우를 만듭니다.
- $f_c$를 가지고 이상적인 필터의 계수 $h_d(n)$을 만듭니다. 이때 필터의 길이는 M입니다.
- 마지막으로 FIR 윈도우 방법과 같은 방법으로 카이저 윈도우에 $h_d(n)$를 곱해서 원하는 필터 $h(n)$을 구합니다.
베셀 함수
아래의 함수는 수렴하는 값을 가지는 수열 베셀 함수입니다. 카이저 윈도우는 이 베셀 함수를 기초로 만들어집니다.
$$I_0(x)=1+\sum_{k=1}^{\infty}\left (\frac{(\frac{x}{2})^k}{k!} \right )^2$$
카이저 윈도우
카이저 윈도우는 다음과 같이 정의됩니다. 여기서 $\alpha$와 $\beta$만 구하면 됩니다.
$$W(n)=\frac{I_0\left (\beta \sqrt{1-\left (\frac{n-\alpha}{\alpha})^2\ \right )} \right )}{I_0(\alpha)}$$
윈도우 길이 M과 $\alpha$
리플 값을 이용해서 A라는 파라미터를 먼저 구합니다.
$$A=-20log10\left ( min(\delta _{pass},\delta _{stop}) \right )$$
그리고 필터의 길이 M은 다음과 같이 구해집니다. 여기서 $\Delta \omega = abs(\omega_{stop}-\omega_{pass})$ 입니다. 만약 M이 짝수이면 이를 M에 가까운 홀수로 만들어 줍니다.
$$M=round(\frac{A-7.95}{2.285\Delta \omega})$$
$\alpha=M/2$로 구합니다.
$\beta$ 구하기
A조건에 따라서 $\beta$를 구합니다.
$$\beta=\left\{\begin{matrix}
0,where (A<21) \\
0.5842(A-21)^{0.4}+0.07886(A-21)), whrere (21\leq A\leq 50)\\
0.1102*(A-8.7),where(A>50)&&
\end{matrix}\right.$$
이제 원하는 이상적 필터를 윈도우 방식으로 구하고, 여기에 카이저 윈도우 W(n)를 곱하면 됩니다.
카이저 윈도으로 LPF 구하기
기존의 윈도우 방식으로 FIR LPF를 구한 내용에서 카이저 윈도우를 적용한 GNU Octave의 스크립트 내용입니다.
#https://www.youtube.com/watch?v=MdhS91q4Pm0&t=46s
clear all;
## 선형적으로 증가되는 주파수를 만든다.
function freq= Make_Lin_Freq(f_min, f_max, vect_size)
freq = zeros(vect_size,i);
df = (f_max-f_min)/(vect_size-1);
tmp = f_min;
freq(1,1)=f_min;
for k=2:vect_size
freq(k,1)=freq(k-1,1)+df;
endfor
endfunction
## 베셀 함수
function sum = Bessel_I0(x)
max_loop = 200;
sum =1;
sum_old = 1;
fract = 1;
tmp = 0;
for k =1:max_loop
fract = fract * k;
tmp = ((x/2)^k/fract)^2;
sum = sum+tmp;
if(sum == sum_old)
return;
endif
sum_old = sum;
endfor
endfunction
## 카이저 윈도우를 위한 파라미터 생성
function [M,beta] = Kaiser_Coef(fs,f_pass,f_stop,dp,ds)
#Ap= 20*log10((1+dp)/(1-ds));
#As = -20*log10(ds);
wp=2*pi*f_pass/fs;
ws=2*pi*f_stop/fs;
wc = (wp+ws)/2;
dw = abs(ws-wp);
d = min(dp,ds);
A = -20*log10(d);
if (A<21)
beta =0;
elseif((A>=21)&&(A<=50))
beta = (0.5842*(A-21)^0.4)+(0.07886*(A-21))
else
beta = 0.1102*(A-8.7);
endif
M=round((A-7.95)/(2.285*dw));
if(mod(M,2)==0)
M=M+1;
endif
#alpha = M/2;
endfunction
## 카이저 윈도우 생성
function W=Kaiser_Window(b,M)
W= zeros(M,1);
a = M/2;
for n = 1:M
num =Bessel_I0(b*(1-(((n-1)-a)/a)^2)^0.5);
W(n)= num/Bessel_I0(b);
endfor
endfunction
## FIR로 이상적인 저역 통과 필터를 만들고 윈도우 적용
function h = LPF(fs,fc,W,N)
h = zeros(N,1);
wc = 2*pi*fc/fs;
M= (N-1)/2;
for n = 0: M
if (n!=M)
h(n+1,1) = sin(wc*(n-M))/pi/(n-M) * W(n+1,1);
nn = (2*M)-n;
h(nn+1,1) = h(n+1,1);
else
h(n+1,1) = wc/pi * W(n+1,1);
endif
endfor
endfunction
## FIR 필터의 주파수 응답 구하기
function mag=Calc_Mag(fs,h,N,freq_vector)
M = (N-1)/2;
mag = zeros(size(h,1),1);
c = zeros(M,1);
for n =0: (size(freq_vector,1)-1)
w = 2*pi*freq_vector(n+1,1)/fs;
tmp =0;
for k=0:M-1
tmp += h(k+1)*cos(w*(k-M));
endfor
mag(n+1,1) =20*log10(abs( h(M+1)+(2*tmp)));
endfor
endfunction
fs = 48000;
f_pass = 10;
f_stop = 1000;
dp = 0.001;
ds = 0.001;
[M,beta] = Kaiser_Coef(fs,f_pass,f_stop,dp,ds);
W=Kaiser_Window(beta,M);
fc = (f_pass+f_stop)/2
h = LPF(fs,fc,W,M);
freq_vector = Make_Lin_Freq(10, fs/2, 5000);
mag=Calc_Mag(fs,h,M,freq_vector);
clf;
semilogx(mag);
ylim([-100,10])
grid on;통과 대역과 저지 대역의 주파수 설정에 따라 필터 모양이 변경됩니다. 여기서 두 주파수의 차이가 작을수록 필터 계수의 수량이 증가합니다.
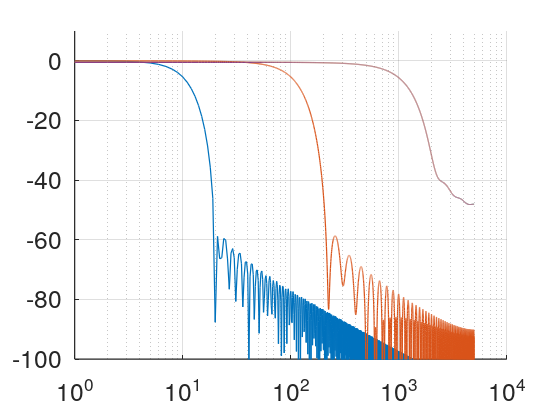
리플에 따라서 저지 대역의 특성이 변경됩니다.
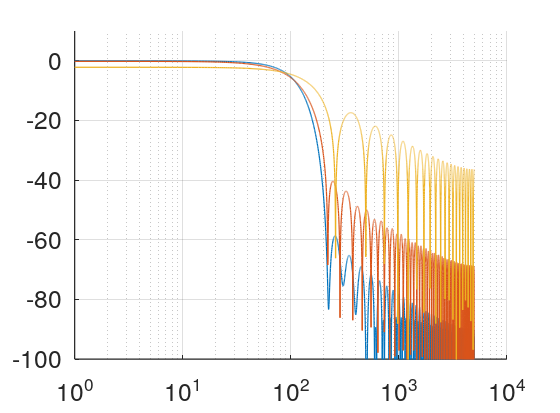
기존의 윈도우 방식과 다르게 필터의 길이 M을 설정하지 않고, 카이저 윈도우를 만들 때 필터 길이가 파라미터로 생성됩니다.
광고좀 꾹 눌러주시면 고맙겠습니다.
위의 내용을 참조용으로만 사용해주세요. 무단 도용이나 무단 복제는 불허합니다.
기타 문의 사항은 gigasound@naver.com에 남겨 주시면 고맙겠습니다.