오디오 필터(14)-IIR 버터워스 고역 통과 필터(Butterworth High Pass Filter) 설계

---

고역 통과 필터 설계

다른 글에서 사용했던 유사한 방법으로 Butterworth HPF를 설계하겠습니다. 이번엔 필터의 Q를 이용하지 않고, 필터의 차단 주파수와 감쇄량을 이용하는 방법을 알아보겠습니다.

 

다음과 같은 조건으로 고역 통과 필터를 만들겠습니다.

• 통과대역의 특성으로 차단 주파수와 통과대역 주파수$f_{c}=F_{p}=1000Hz$로 하겠습니다.
• 그러면 $F_{p}$ 에서 감쇄량은 -3dB가 됩니다.
• 그리고 저지 대역의 주파수 $F_{s}=80Hz$이며 감쇄량이 -80dB입니다.
• 이때 샘플링률 $f_{s}=44100Hz$, 샘플 구간 $T_{s}=1/f_{s}$입니다. 

 

---

필터의 전달 함수 구하기

먼저 필터의 조건으로 다음과 같이 필터를 계산하기 위한 사전 조치를 취합니다.

$$A_{p}=10^{\left | \delta_{p}/10 \right |}$$

$$A_{s}=10^{\left | \delta_{s}/10 \right |}$$

$$\omega_{p}=2\pi F_{p}$$

$$\omega_{s}=2\pi F_{s}$$

$$\Omega_{p}= 2/T_{s} tan\left ( \omega_{p}T_{s}/2 \right )$$

$$\Omega_{s}= 2/T_{s} tan\left ( \omega_{s}T_{s}/2 \right )$$

그런 다음 조건에 부합하는 필터 차수 N을 다음식으로 구합니다. 여기서 ceil()은 올림 정수를 구하는 함수입니다.

$$N=ceil\left (\frac{1}{2} \frac{log((A_{s}-1)/(A_{p}-1))}{log(\Omega_{p}/\Omega_{s}))} \right )$$

그리고 N에 의해 $\omega_{c}=1$인 조건에 정규화된 버터워스 필터의 전달 함수를 선택합니다.

$$N==1\rightarrow H(s)=\frac{1}{s+1}$$

$$N==2\rightarrow H(s)=\frac{1}{s^{2}+\sqrt{2}s+1}$$

$$N==3\rightarrow H(s)=\frac{1}{(s+1)(s^{2}+s+1)}$$

$$N==4\rightarrow H(s)=\frac{1}{(s^{2}+0.76537s+1)(s^{2}+1.8477s+1)}$$

$H(s)$를 $s\rightarrow \Omega_{c}/s$로 치환해서 정규화된 필터를 HPF로 변경합니다.

이를 디지털 필터로 변환하기 위해서 또다시

$$s\rightarrow \frac{2}{T_{s}}\frac{z-1}{z+1}$$로 치환해서 $H(s)$를 $H(z)$로 변경합니다. 

이 방법은 주워진 조건을 최대한 만족하는 필터의 전달 함수를 구해줍니다.

---

필터 계수 구하기

다음과 같이 필터 계수를 구하고 특성을 확인하는 GNU Octave의 스크립 파일을 만듭니다.

##
# butterworth HPF filter using BLT
##
clc;
clear all;
## FFT
NFFT = 2^12;
## load package
pkg load signal;
pkg load symbolic;
## symbol
z = sym('z','complex');
s = sym('s','complex');
## sampling rate
fs = 44100.0; #Hz
# sample time
Ts = 1.0/fs; #second
#frequency
fp = 1000.0; #Hz
fs = 80.0; #Hz
wp = 2.0*pi*(fp) #rad/s
ws = 2.0*pi*(fs) #rad/s
wc = wp
#prewaping frequency
Wp = 2.0/Ts * tan(wp*Ts/2.0);
Ws = 2.0/Ts * tan(ws*Ts/2.0);
Wc = Wp;
#attenuation
delta_p = -3.0; #dB
delta_s = -80.0; #dB
Ap = 10.0^abs(delta_p/10.0);
As = 10.0^abs(delta_s/10.0);
N_num = log10((As-1)/(Ap-1));
N_den = log10(Wp/Ws);
N = 0.5*N_num/N_den;
N=ceil(N)
#Hs_den = 1;
if(N==1)
  Hs_den = s+1;
elseif(N==2)
  Hs_den = s^2+ sqrt(2)*s + 1;
elseif(N==3)
  Hs_den = (s+1)*(s^2+s+1);
elseif(N==4)
  Hs_den = (s^2+0.76536*s+1)*(s^2+1.8477*s+1);
else
  return
endif
Hs=1/Hs_den;
#subsitution
Hs = subs(Hs,s,(Wc/s));
Hs = simplify(expand(Hs));
#BLT
zb = 2.0/Ts * (z-1) /(z+1);
Hz = subs(Hs,s,(zb));
Hz = simplify(expand(Hz));
#filter coeffieient
[num_z,den_z]= numden(Hz);
coeff_b = coeffs(num_z,z,'all');
coeff_a = coeffs(den_z,z,'all');
coeff_num = double(coeff_b);
coeff_dev = double(coeff_a);
##Coefficient normalization
a0 =  coeff_dev(1);
coeff_num /= a0
coeff_dev /= a0
#display 
figure(1);
clf;
zplane(coeff_num,coeff_dev);
figure(2);
clf;
subplot(2,1,1);
[h,w] = freqz(coeff_num,coeff_dev,NFFT,fs);
m = 20.0*log10(abs(h));
semilogx(w,m);
#xlim([20 fs/2]);
ylim([-60 10])
xlabel("frequency(Hz)")
ylabel("magitude(dB)")
grid();
subplot(2,1,2);
semilogx(w,arg(h)*180/pi);
#xlim([20 fs/2]);
ylim([-200 200])
xlabel("frequency(Hz)");
ylabel("phase(deg)");
grid();

butter_blt_hpf_3.m

0.00MB

---

필터 특성 검토

z-영역에서 필터의 특성은 다음과 같습니다. 모든 극점이 단위원 안에 있어 안정적입니다.

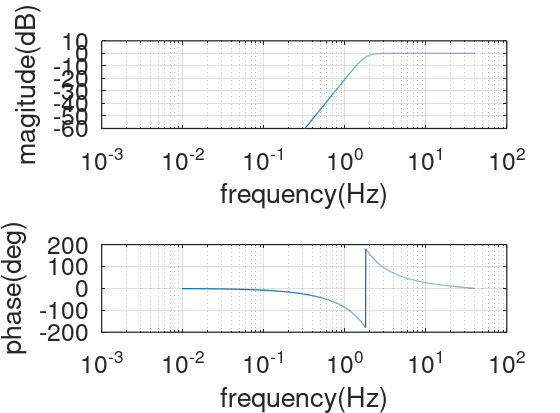
주파수 특성은 다음과 같습니다. 고역 통과 필터가 형성되어 있습니다.

 

---

광고좀 꾹 눌러주시면 고맙겠습니다. 

---

위의 내용을 참조용으로만 사용해주세요. 무단 도용이나 무단 복제는 불허합니다.

기타 문의 사항은 gigasound@naver.com에 남겨 주시면 고맙겠습니다.