오디오 신호의 변화 특성
잡음 신호등의 인공적인 신호를 제외하고 음성과 악기는 아래 그림과 같이 시간에 따라 신호가 변화합니다. 이런 신호의 변화 형태를 포락선(envelope)이라 하고, 포락선에 따라 신호처리를 하는 방식을 다이내믹 처리(dynamic processing)라고 합니다.
그러므로 다이내믹 신호처리를 위해서는 포락선을 검출하는 내용이 필요하고 사실 매우 중요한 역할을 합니다.
이글에서는 오디오 신호의 변화인 포락선을 어떻게 검출하는지 알아보겠습니다.
오디오 신호 변화의 구간
아래의 신호의 그래프는 절댓값 또는 데시벨로 신호를 표시한 내용으로 이를 포락선(envelope)이라고 합니다. 다이내믹 처리는 사실 포락선을 구하고, 어떤 포락선 상태에 있는지에 따라 신호를 처리하는 방법을 달리합니다. 그러므로 포락선을 검출하는 방법을 먼저 알아볼 필요가 있습니다.

오디오 신호는 소리의 발성이 시작된 구간에서 종료되는 구간까지 총 4개의 구간으로 분류 가능합니다. 물론 음성과 악기 및 악기의 연주 방법 그리고 주변 환경에 영향으로 생략되는 구간도 있습니다만, 대부분 아래의 4개의 구간으로 표시할 수 있습니다.
- 어택(attack) 구간 : 소리가 시작돼서 초기에 가장 큰 소리로 발전하는 구간입니다.
- 디케이(decay) 구간 : 어택 이후 소리가 줄어드는 구간입니다. 이 구간이 없을 수도 있습니다. 특히 관악기 중 일부와 연주 방식에 따라 이 구간이 없기도 합니다. 어택과 디케이를 합쳐 초기 구간이라고 합니다.
- 서스틴(sustain) 구간 : 초기 구간의 신호를 지속적으로 유지하는 구간입니다. 신호의 크기가 다소 줄 수는 있어도 청감적으로는 같은 소리로 들립니다. 이 구간이 없거나 아주 짧을 수 있는데 음악 연주에서 스타카토(staccato) 기법에 해당합니다. 반대로 긴 서스틴 구간을 만들기도 하는데 파이프 오르간에서 계속 건반을 누르거나 피아노 등에서 서스틴 페달을 누른 것과 같습니다.
- 릴리즈(release) 구간 : 소리의 크기가 청감적으로 느껴질 정도록 감소하는 구간입니다. 이 구간은 일차적으로 소리 음원에 의해 결정되지만 잔향의 영향으로 구간이 길어질 수도 있습니다.
시정수
정말 뜬금없이 회로에 대해 얘기 해야겠습니다. 이는 시정수 (time constant, $\tau$)를 다뤄야 하기 때문입니다. 시정수는 회로가 신호의 변화에 대해 얼마나 빨리 대응해서 최종 값에 도착하는지 알 여주는 값입니다.
즉 시정수가 작을수록 신호가 변화에 빠르게 대응해서 변한 신호에 접근할 수 있음을 의미합니다. 신호처리에서도 이 개념을 그대로 사용합니다.
시정수를 정의하기 위해서 다음과 같은 회로의 동작을 먼저 이해해야 합니다. 아래 회로는 QucsStudio로 구현했습니다. 저항 하나와 케패시터로 구현되어 있으며 출력은 케페시터에서 얻어집니다. 입력 신호는 구형파입니다.

그러면 출력 신호의 일부는 다음과 같이 보입니다. 0.2초에서 입력 신호인 구형파가 1V -> 0V로 변해도 출력 신호는 케패시터의 영향으로 점차 감소합니다. 이 감소 곡선은 $V_{out}(t)=e^{\frac{-t}{R_1 C_1}}$ 형태로 지수함수이며 특성은 $R_1$, $C_1$의 곱으로 나타납니다.
그리고 $\tau = R_1 C_1$으로 정의됩니다. 즉, 지수함수로 감쇠되는 정도를 $\tau$로 결정할 수 있습니다.

그런데 $\tau$는 최종 값의 63%에 해당하는 위치의 시간으로 $1-e^{-1}$의 값에 해당합니다. 이를 고려하면 $3\tau = 0.95$로 최종 값의 95%에 도달했다는 의미입니다.
위의 회로에서 1V -> 0V의 63%인 전압은 0.37V이며 시간은 200ms -> 210ms로 10ms의 시간이 걸렸습니다. 시정수를 계산해 보면 $\tau = R_1 C_1 = 10ms$입니다.
시정수를 알면 이 값의 3배에 최종 값에 도달한 것으로 간주해되 된다는 의미입니다. $3\tau = 30ms$에서 전압은 95%에 해당하는 값이네요.

$C_1 = 200 \mu F$로 고치면, $\tau = R_1 C_1 = 20m$s입니다. 아래의 결과를 보면 계산 값과 같습니다.

시정수는 신호가 끝난다음 변화하는 방법을 제공해줍니다. 즉 시정수는 시간에 따라서 변화하는 신호의 특성을 제공해 주기 때문에 시정수를 정의해서 신호의 변화를 얼마나 빠르게 또는 느리게 반영할지 결정하게 됩니다.
이를 이용해서 오디오 신호의 변화를 반영하는 곡선을 만들 수 있기 됩니다. 세부적으로는 위의 회로와 유사한 형태의 특성을 가지는 차분 방적식에 시정수를 도입해서 포락선을 검출하는 방법을 만듭니다.
차분 방정식을 이용한 포락선 검출
오디오 신호가 시간에 따라 포락선을 구할 수 있는데 이를 최외곽 포락선(outermost envelope)이라고 부르겠습니다. 그런데 최외곽 포락선은 오디오 신호가 빠르게 변화하기 때문에 이를 이용해서 신호 처리하기에는 부적합합니다. 그래서 이전 글에서 다루웠던 차분 방정식을 이용한 평균기를 이용해서 다소 변화를 둔화시킨 포락선 검출을 합니다.
아래의 차분 방적식을 다음과 같이 조정하여 시정수 (time constat, $\tau$)에 의해 이동 평균을 구하는 식을 사용하겠습니다. 여기서 시정수는 과거 신호와 현재 신호의 차이를 얼마나 현재에 반영할지 결정합니다. $\tau =1$이면 입출력 신호 차이를 그대로 출력에 반영합니다. $\tau =0$ 이면 신호의 변화 내용을 반영하지 않습니다.

$$y[n]=x[n]+\tau (y[n-1]-x[n])$$
여기서 $\tau = exp(-1/(\alpha \cdot f_s))$로 하고, $f_s$는 신호처리의 샘플률, $\alpha$를 포락선을 구하기 위한 계수로 사용합니다. 즉 $\alpha$는 위의 회로에서 RC에 해당하게 됩니다. 신호 처리과정에서 $\alpha$는 신호의 감쇄 정도를 시간의 양으로 표시하는 역할을 하게 됩니다.
wav에서 일부 읽어서 표시하기
GNU Octave로 포락선 y[i]를 출력해 보겠습니다. 다음 스크립트는 wav에서 일부 구간을 읽어서 표시해 줍니다.
clear all
file_name = 'test.wav';
[xx,fs]=audioread(file_name);
fs = 44100;
start_x = 35000;
gap = 10000;
end_x = start_x + (gap-1);
x = xx(start_x:end_x,1);
clf
plot(x,'g');
ylim([-0.3 0.3]);
grid on;
$\alpha$를 이용한 포락선 검출
포락선 검출을 위한 전체 스크립트 내용이며 먼저 $\alpha = 1.0 \mu$sec 조건으로 실행해 보겠습니다.
clear all
file_name = 'test.wav';
[xx,fs]=audioread(file_name);
fs = 44100;
alpha = 1 * 10^-6;
tau = exp(-1/ alpha/fs);
start_x = 35000;
gap = 10000;
end_x = start_x + (gap-1);
x = xx(start_x:end_x,1);
env= abs(x(1,1));
for i = 1 : gap
tmp = abs(x(i));
env = tmp + (tau*(env-tmp));
y(i,1) = env;
endfor
clf
plot(x,'g');
hold on
plot(y,'r');
ylim([-0.3 0.3]);
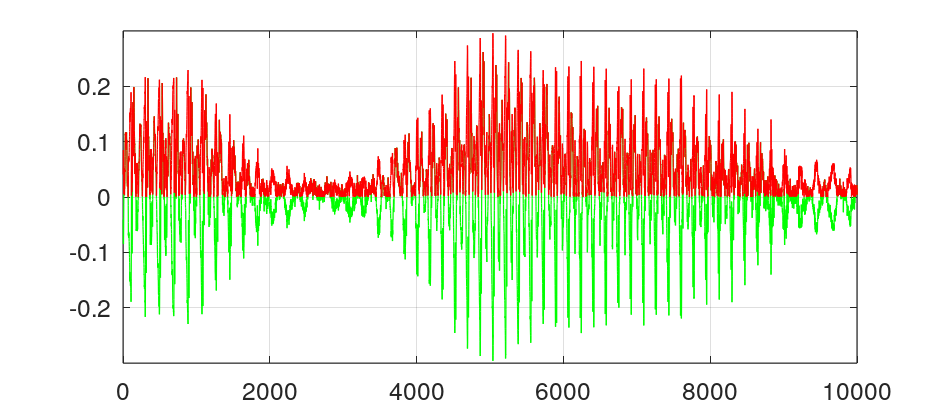
grid on;붉은색 부분이 포락선인데, 신호를 그냥 절댓값으로 표시하여 최외곽선 포락선을 구한 것처럼 보입니다. 다른 조건을 사용해야겠네요.
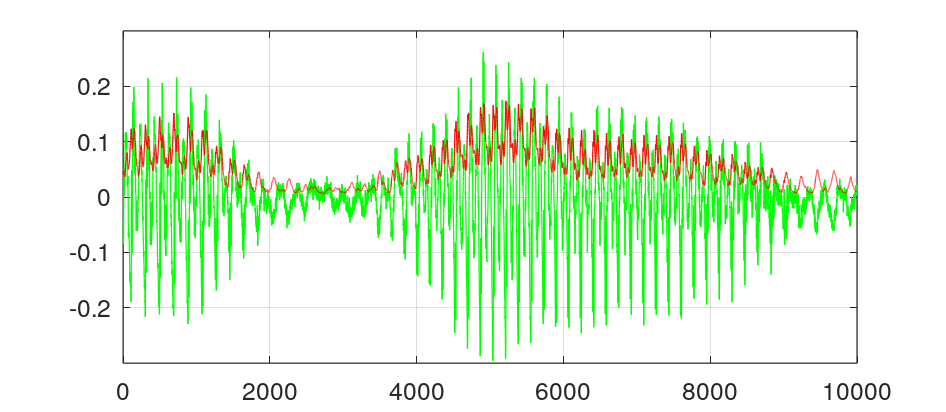
$\alpha = 500 \mu$sec인 조건입니다. 신호의 뾰족한 피크 신호를 무시하고 신호의 크기 변화를 반영하는 것으로 보입니다. 좀 더 개선해 보겠습니다.
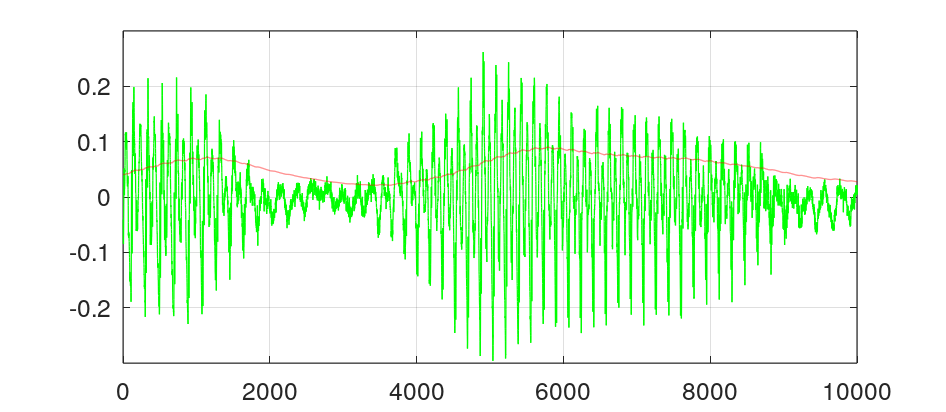
$\alpha = 20m$sec인 조건입니다. 피크 신호는 완전히 무시되었고 신호의 크기 변화만 잘 반영하고 있습니다. 이 정도이면 오디오의 다이내믹 처리용으로 사용할 수 있습니다.
사실 다이내믹 처리는 오디오 신호의 추이가 증가인지 감소인지가 중요한 정보로 사용됩니다. 세세한 신호의 변화는 오히려 신호처리에 좋지 않은 영향을 줍니다.
$\alpha = 200m$sec인 조건입니다. 너무 과도한 조건을 사용해서 포락선 정보로 사용하기 어렵습니다.
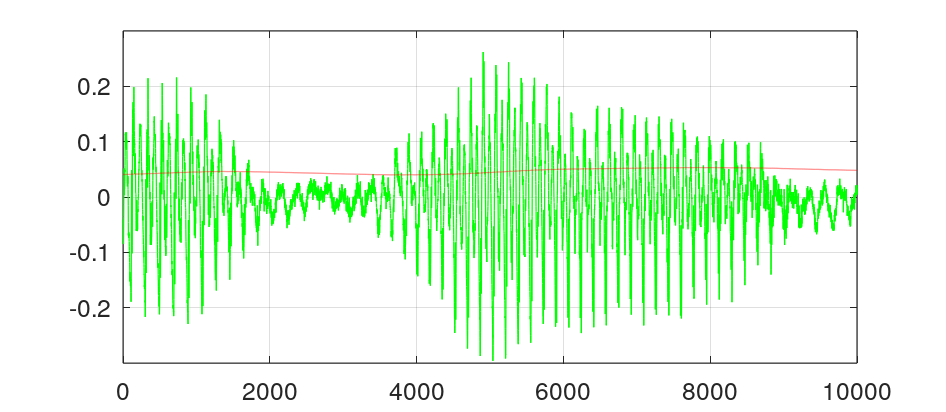
포락선 추출은 특별한 값으로 정하기 어렵습니다. 왜냐하면 입력 신호의 특성이 따라 추출되는 포락선 특성이 다르기도 하고, 사용 용도에 따라서 적합한 추출 내용도 다르기 때문입니다.
광고좀 꾹 눌러주시면 고맙겠습니다.
위의 내용을 참조용으로만 사용해주세요. 무단 도용이나 무단 복제는 불허합니다.
기타 문의 사항은 gigasound@naver.com에 남겨 주시면 고맙겠습니다.
'Audio Processing' 카테고리의 다른 글
| 다이내믹 신호처리(4)-어택과 릴리즈를 고려한 포락선 검출 (0) | 2021.10.21 |
|---|---|
| 다이내믹 신호처리(3)-실효치 포락선, 피크 포락선 (0) | 2021.10.21 |
| 다이내믹 신호처리(1)-개요 (0) | 2021.10.21 |
| Python의 FFT, 평균화(averaging), 평활화(Smooth) (1) | 2021.09.28 |
| 신호처리를 위한 평균 (0) | 2021.09.28 |



