오디오 필터(2)-바이쿼드 필터 (Bi-quad Filter), s 영역, z영역, 필터의 안정성

---

신호처리와 필터 계수

오디오 처리에서는 다양한 필터를 사용합니다. 그런데 이 필터를 설계하고 최종적으로 얻고자 하는 것이 무엇일까요?  한마디로 필터의 계수를 구하고자 노력하는 것입니다. 이렇게 얻어진 필터 계수들은 IIR 또는 FIR 필터에 의해 실제 신호에 필터 특성을 부가한 결과를 얻게 되고 이 결과가 우리가 신호처리를 하는 과정입니다. 

그러므로 필터 계수를 어떻게 얻을지에 목표를 삼으면 됩니다. 여기서는 오디오 필터에서 가장 많이 사용되는 필터 전달 함수인 바이쿼드 필터에 대해서 알아보고 s영과 z영역에 대해서도 알아보겠습니다. 

---

아날로그 신호를 표현하는 s영역

전자공학에서 미분과 적분을 많이 사용합니다. 이 중에서 적분이 회로를 해석할 때 어려움을 주게 됩니다. 그래서 좀 더 편리하게 회로를 해석하기 위해서 라플라스 변환(Laplace' transform)을 사용합니다. 신호 $f(t)$에 대한 라플라스 변환은 다음과 같이 정의됩니다. 즉 라플라스 변환은 신호를 무한한 시간 동안 $e^{-st}$의 가중치로 적분합니다. 그러로  $f(t)$가 발산하지 않는 한 안정적으로 수렴하고 이 값을 $F(s)$로 표시하는 것입니다. 이때 라플라스 변환에는 주파수에 관한 내용이 겉으로 나타나 있지는 않습니다. 왜냐 하면 s는 복소수로 취급하기 때문에  $e^{-st}$는 오일러 공식에 의해 정현파를 의미하기 때문입니다.

$$F(s)=\int_{0}^{\infty } e^{-st}f(t)dt$$

라플라스 변환에서 s가 복수 이므로 $F(s)$는 복소수 공간에 s에 따라 궤적을 그릴 수 있습니다. 이 복소수 좌표를 특별히 s 공간이라고 부릅니다. 그리고 $F(s)$의 값들이 좌반구에 있으면 안정적이라고 판단합니다. 즉 $F(s)$의 실수부가 모두 음의 값을 가지고 있어야 한다는 뜻입니다. 불안정하면 신호는 신호이 따라 발산하게 됩니다. 

그러므로 회로나 어떤 신호가 안정적인이 아닌지는 라플라스 변환을 해보면 알 수 있습니다. 오디오 필터가 안정하지 못하면 필터가 신호를 급격히 증폭하여 엄청난 오류가 발생하게 됩니다. 그러나 변환을 꼭 해서 확인해야겠죠.  

---

전달 함수

전달 함수(Trasfer function)는 입력된 신호와 출력된 신호의 비율을 표시하여 필터의 특성을 표시하는 아주 유용한 방식입니다. 

$$h(t)=\frac{f_{o} (t)}{f_{i} (t)}$$

이보다는 s영역으로 변환해서 사용하는 것이 더욱 편리합니다. 여기서 $\mathfrak{L}$는 시간축 신호를 라플라스 변환하는 표식입니다. 

$$H(s)=\mathfrak{L}\left ( h(t) \right )=\frac{H_o (s)}{H_i (s)}$$

---

s영역과 f영역

푸리에 변환(Fourie transform)은 다음과 같이 정의되어 있습니다. 이는 시간축 신호를 주파 축으로 변환하여 표시합니다. 

$$F_f(f)=\int_{-\infty  }^{\infty}e^{-j2\pi ft}f(t)dt$$

이를 라플라스 변환식과 비교하면 $s=j2\pi f$로 표시되는 것과 같습니다. 즉 s 영역에서 붉게 표시된 허수 축을 따라서 적분하는 것과 같습니다. 그러므로 푸리에 변화는 라플라스 변환의 일부입니다.  

---

z변환과 z영역

z변환은 샘플링에 의해 구해지는 불연속적인 신호를 라플라스와 같은 변환으로 편리하게 사용하고자 만든 내용입니다. 그러므로 사용되는 신호는 연속 함수 $f(t)$를 샘플링한 x(n)이 됩니다. 여기서 n는 샘플링에 의해 구해진 n번째 신호로 샘플링 시간은 샘플링률 $f_s$Hz의 역수  $t_s=1/f_s$입니다. 

z변환은 다음과 같이 정의됩니다.

$$X(z)=\sum_{-\infty }^{\infty}x(n)z^{-n}$$

라플라스 변환과 z변환을 비교하면 다음과 같이 내용으로 정리가 됩니다. 

$$z=e^{j2\pi f/f_s}$$

여기서 $f_s$에 의해 주파수의 영역이 제한됩니다. 즉 f가 아무리 변해도  $f_s$값 이하가 되도록 조정됩니다. 그렇게 되면 s영역의 허상 축(붉은색)은 단 위원으로 변경되고, 단위원 안은 s 영역의 좌반구에 해당하게 됩니다. 이제 우리는 s영역의 특성을 z 영역에서는 단 위원을 기준으로 z변환 결과를 검토하여 안정성을 판단하면 됩니다. 

---

IIR 바이 쿼드 필터

바이 쿼드 필터(bi-quad filter)는 IIR 디지털 오디오 필터를 구현하는 매우 기초적 형태를 나타냅니다.  신호처리 과정에서 출력 신호는 다음과 같이 표시됩니다.

$$y[n]=\sum_{i=0}^{M-1}\left (\beta _{i}\cdot x[n-i]  \right )-\sum_{i=0}^{N-1}\left (\alpha _{i}\cdot y[n-i]  \right )$$

이식을 z 변환한 다음에 입력과 출력의 비율로 정리하면 필터의 전달 함수가 됩니다. 이때 2차 식으로 표시되는 전달 함수를 bi-quad 필터라고 부릅니다. 그리고 ${\alpha_{i}}, {\beta_{i}}$를 필터 계수라고 부릅니다. 그리고  ${\alpha_{0}}$로 계수를 나누고 구한 필터 계수를 ${a_{i}}, {b_{i}}$로 정의해서 사용합니다. 그러면 5개의 필터 계수만 고려하면 됩니다. 

$$H(z)=\frac{Y(z)}{X(z)}=\frac{\beta_0+\beta_1z^{-1} +\beta_2z^{-2}}{\alpha_0+\alpha_1z^{-1}+\alpha_2z^{-2}}=\frac{b_0+b_1z^{-1} +b_2z^{-2}}{1+a_1z^{-1}+a_2z^{-2}}$$

이때 $X(z)=0$를 $H(z)$의 극점 방정식 또는 특성 방정식이라고 합니다. 극점 방정식이 2차 이므로 두개의 근을 가지고 이 근이 극점(pole)이 됩니다. 

 또한 $Y(z)=0$를 $H(z)$의 영점 방정식으로 이 방정식의 근이 영점(zero)이 됩니다. 

이중에서 극점이 z엉역의 단위원 안에 있어야 방정식 즉 필터가 안정적이라고 판별합니다. 

---

이 필터는 다음과 같을 때 안정적입니다.

$$\left | a_{2} \right |<1$$

$$\left | a_{1} \right |<a_{2} +1$$

---

GNU Octave를 이용해서 구해진 필터 계수가  안전한지, 주파수 출력이 원하는 특성인지 검토할 수 있습니다.

# pole-zero plan
figure(1)
clf
zplane(b,a)
# magnitude response
[h,w] = freqz(b,a,NFFT,SAMPLING_RATE);
m =20.0*log10(abs(h));
figure(2);
clf
subplot(2,1,1)
semilogx(w,m)
xlim([20 44100/2])
ylim([-40 10])
xlabel("frequency(Hz)")
ylabel("magitude(dB)")
grid()
# phase response
subplot(2,1,2)
semilogx(w,arg(h)*180/pi)
xlim([20 44100/2])
ylim([-200 200])
xlabel("frequency(Hz)")
ylabel("phase(deg)")
grid()

 

---

필터 특성의 검토

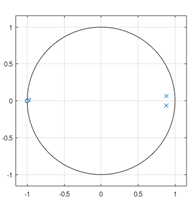
z영역에서 필터의 극점 상태를 다음과 같이 얻을 수 있습니다. 극점이 단위원 안에 있으면 필터는 안정적입니다. 그러니 필터의 계수를 구하고 이를 GNU Octave와 같은 툴을 이용해서 z영역에서의 특성을 표시하면 됩니다.

만악 원한다면 오디오 주파수 대역에서 극점의 변화를 전부 표시해서 한꺼번에 안정성을 확인할 수 있으며, 이를 root locus라고 합니다. 

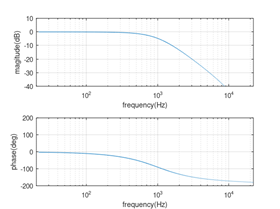
다음과 같이 진폭 응답과 위상 응답도 구할 수 있습니다.

---

광고좀 꾹 눌러주시면 고맙겠습니다. 

---

참조

http://shepazu.github.io/Audio-EQ-Cookbook/audio-eq-cookbook.html

---

위의 내용을 참조용으로만 사용해주세요, 무단 도용이나 무단 복제는 불허합니다.

기타 문의 사항은 gigasound@naver.com에 남겨 주시면 고맙겠습니다.